[알고리즘] 플로이드 워샬 알고리즘
2015. 7. 11. 16:23ㆍ프로그래밍/알고리즘
728x90
728x90
서론
그리 어려운 알고리즘이 아니라서 위키를 파워 활용하여 정리해보자!
정의
플로이드-워셜 알고리즘(Floyd-Warshall Algorithm})은 그래프에서 모든 꼭짓점 사이의 최단 경로의 거리를 구하는 알고리즘이다. 음수 가중치를 갖는 변도 순환만 없다면 잘 처리된다. 제일 바깥쪽 반복문은 거쳐가는 꼭짓점이고, 두 번째 반복문은 출발하는 꼭짓점, 세 번째 반복문은 도착하는 꼭짓점이다. 이 알고리즘은 플로이드 알고리즘이라고도 알려져 있다.
복잡도
플로이드-워셜 알고리즘으로 모든 정점 간 경로의 최소비용을 구하는 것은 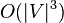 의 시간 복잡도를 갖는다. 경유지를 기록한 경우, 경로를 역으로 추출하는 알고리즘의 복잡도는
의 시간 복잡도를 갖는다. 경유지를 기록한 경우, 경로를 역으로 추출하는 알고리즘의 복잡도는  의 시간 복잡도를 갖는다. 종종 다익스트라 알고리즘과 자주 비교되곤 하는데, 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정 필요성이 요구된다.
의 시간 복잡도를 갖는다. 종종 다익스트라 알고리즘과 자주 비교되곤 하는데, 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정 필요성이 요구된다.
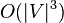 의 시간 복잡도를 갖는다. 경유지를 기록한 경우, 경로를 역으로 추출하는 알고리즘의 복잡도는
의 시간 복잡도를 갖는다. 경유지를 기록한 경우, 경로를 역으로 추출하는 알고리즘의 복잡도는  의 시간 복잡도를 갖는다. 종종 다익스트라 알고리즘과 자주 비교되곤 하는데, 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정 필요성이 요구된다.
의 시간 복잡도를 갖는다. 종종 다익스트라 알고리즘과 자주 비교되곤 하는데, 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정 필요성이 요구된다.코드
수도코드와 예제 코드를 이용해서 직접 작성해보았다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 | #include <stdio.h> #define N 4 #define INF 10000 // Cost Table. d[v1][v2] : Minimum cost of path v1 -> v2 int d[N][N]; // via table int via[N][N] = { {0, 3, INF, INF}, {INF, 0, 12, 6}, {INF, 5, 0, 7}, {2, 9, 4, 0}, }; void doFloyd() { // Initialize for (int i = 0; i < N; ++i) { for (int j = 0; j < N; ++j) { d[i][j] = via[i][j]; // k = 0 } } // Do Floyd-Warshall Algorithm for (int k = 0; k < N; ++k) { for (int i = 0; i < N; ++i) { for (int j = 0; j < N; ++j) { if (d[i][j] > d[i][k] + d[k][j]) { d[i][j] = d[i][k] + d[k][j]; via[i][j] = k; } } } // print printf("k = %d \n", k); for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { if (d[i][j] == INF) { char* infString = "INF"; printf("%-6s", infString); continue; } printf("%-5d ",d[i][j]); } puts(""); } puts(""); } } int main() { doFloyd(); } | cs |
결과
그래프
(2017/01/07) 그림 수정. 1->2 가중치와 2->1 가중치가 반대로 되어있던 것 수정(ㅇㄹㅇㄹ님 제보)
k에 따른 테이블 변화
728x90
반응형
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| Project Euler Problem8 (0) | 2015.02.28 |
|---|---|
| Project Euler Problem16 (0) | 2015.02.24 |
| Project Euler Problem15 (0) | 2015.02.17 |
| Project Euler Problem10 (0) | 2015.02.15 |
| Project Euler Problem9 (0) | 2015.02.15 |
| Project Euler Problem5 (0) | 2015.02.12 |
| Project Euler Problem7 (0) | 2015.02.05 |

